Survival Analysis
Explanations & examples: If the data in your text file looks like this:
If the data in your text file looks like this: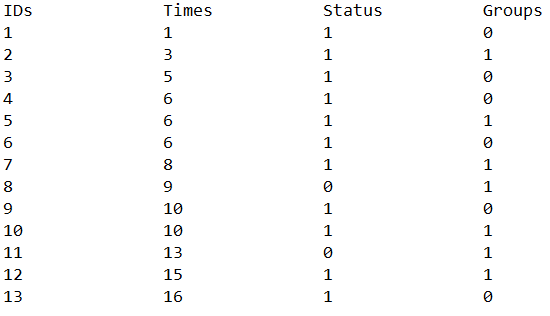 Then you should choose the option "data in file is in columns" to the right when copy/pasting or uploading into the table. If, on the other hand, the data in your text file looks like this:  Then you should choose the option "data in file is in rows" to the right when copy/pasting or uploading into the table. In survival analysis we follow one or more groups over time to watch their survival and survival rates compared with each other. Each row in the input table is a person/patient with an optional ID number. The time of each person is the duration of time that the persons has been observed in the study, calculated in weeks, days, months or another unit. The status can be either 1 = outcome or 0 = censored. The outcome of interest in survival analysis is usually death, but not always. It could also be "getting sick" or even "having recovered". The data studied in survival analysis is usually people, but could also be for eg. machinery. In this case the outcome would be "failure" or similar. When a person is censored at a certain time period in survival analysis, it means that the person leaves the study (is lost to follow-up) for various reasons and that further info about this person therefore is unknown. Within each group, data is sorted after the survival times in ascending order. If more than one event occurs at a given time, the cases are added together. In this way we achieve the life tables of all the groups involved in the study. In the life table of a group, the times at which events occur are listed to the left. For each time (row) the no. of deaths and censored at this time period are listed together with the persons at the start of the period and the no. at risk at this time period. The no. at risk will decrease throughout the table as more and more leave (die or get censored). The risk of dying, r, at a given time period is the number of deaths at that time period divided by the no. at risk at start of the period. The probability of surviving through the time period in question is s = 1 - r. The cumulative survivor function S(t) at a specific time period is all the individual probabilities of survival at the times periods multiplied together up to and including the time period in question (ti). S(t) for that specific time period is then the probability of surviving up to and beyond this time period. The last S(t) is the probability of surviving through the entire period of the study. This number is often 0 (if all the patients died throughout the study), but not necessarily. For each specific S(t) its corresponding 95 % confidence interval is calculated. For more infos and formuls, see the page with the formulas. 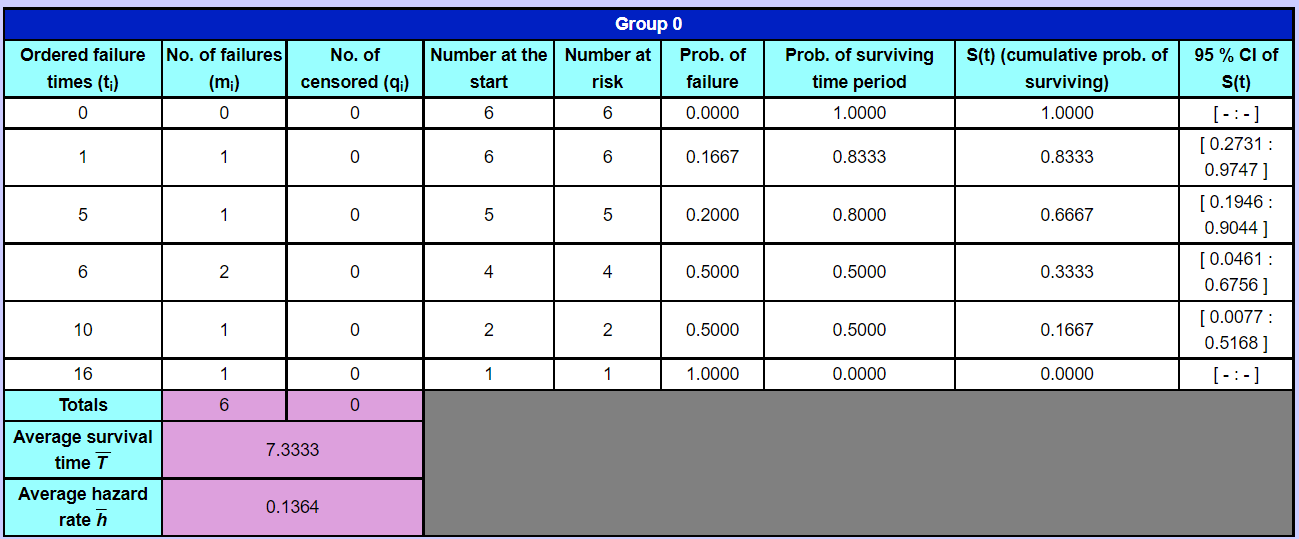 The first row in the cohort life table will be time 0, even though they may be no events at this time. If there are no deaths, the survivor function S(t) will be 1 (or 100%) at this time, because all survived through this period. For each row the number at risk is changing by subtracting the deaths and censored from the previous row. The reason why only half of the censored are being withdrawn from the number at risk is that the time periods in this version of the life tables are usually time intervals of length 1. In other words, the times are often 1,2,3,4,5, ... etc. Since it's unknown at what time during the interval the censored occured, the no. at risk will then theoretically change throughout the interval. It's assumed, therefore, that all the censored occur on average halfway through the interval. The average survival time is the average of all the survival times of the persons in the group (excluding the censored). The average hazard rate is the total no. of deaths in the group (excluding censored) divided by the sum of the survival times in the group. The average hazard rate ratio between two groups (calculated under the life tables) is the average hazard rate for one group divided by the average hazard rate for the other group. It tells how many times a higher rate the first group has compared with the second. These descriptive statistics provide only an overall comparison and don't compare the groups at different times during follow-up. The survival curve can be drawn with the times on the x-axis and the probabilities of S(t) on the y-axis. The Kaplan-Meier estimates and the Kaplan-Meier curves are mostly used, when the time periods in the groups are not intervals of the same length, but for instance 15, 18, 20, 25, 29, ... Then a Kaplan-Meier estimate table can be drawn and the survivor function S(t) calculated for each row (time) t. The Kaplan-Meier curve will be a step function that is constant between two consecutive times and then drops to a lower probability at the next time value in the table. If the curve of one group lies below the curve of another group, then the group with the underlying curve will have a higher hazard rate than the other group. 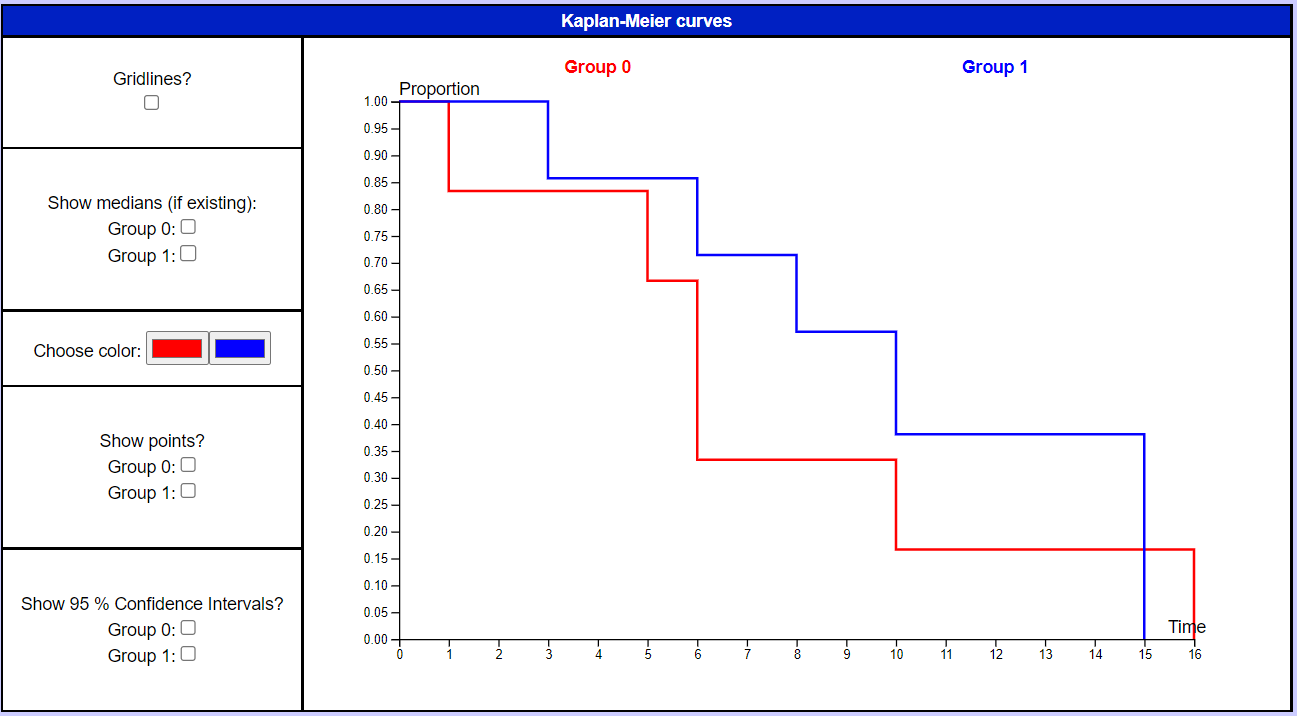 The Mantel-Cox estimate of the hazard ratio can be calculated between two groups by selecting which two in the drop-down selector box. It is an assumption for calculating this rate ratio that the ratio is constant during the time of the study. The interpretation of the Mantel-Cox estimate of the hazard ratio between group 1 and group 2 (group 1 relative to group 2) is that the hazard of dying for group 1 was that many times higher (or lower) than the hazard of group 2 at baseline. It can be tested whether the rates of two groups can be assumed the same, in other words; whether the Mantel-Cox hazard ratio could be equal to 1. This is done with the log-rank test, which is a chi-squared-test with the chi-sqared test statistic χ2 and the corresponding p-value. If p < 0.05 we reject the null hypothesis H0 that HRMC = 1, in other words we reject that the hazard rates could be equal on a five percent significance level. |
No. of rows: |
Decimals:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||