Stratified Analysis
Explanations & examples:
In stratified analysis we stratify the data (divide into two or more strata = "layers") in order to check whether the
variable that we stratified after is an effect modifier or a confounder or none of they two (something cannot be
both an effect modifier and a confounder at the same time). If it's detected that the variable stratified after is a confounder
we adjust for the confounder by calculating the weighted estimate (weighted average) of all the strata. This
adjusted value of either the Risk Ratio, Odds Ratio, Incidence Rate Ratio or Mean Difference is then the effect that the exposure
has on the outcome, after having adjusted for the confounding effect of the confounder.
Input types: If you already have the data in 2 × 2 tables, you should choose the default input type "2 × 2 tables". If, on the other hand, you have the data as unanalysed data in a text file, you should choose input type "raw data". Furthermore; if the data in your text file is in the following format:  then you should also mark the click option "data in file is in columns" before copy/pasting into the table or reading from a data file. If the data in your text file have the following format;  Then you should instead click the check mark "data in file is in rows" before copy/pasting or reading from a data file. Example: The proceedings to detect if a variable is an effect modifier, a confounder or neither is as follows: We use a made-up example to see whether smoking status is an effect modifier or a confounder for the connection between having pets in the household and getting POI (Post-Operative Infection after discharge from hospital). We begin with the "crude" 2 × 2 table without any stratification:  As can be seen in the table, 60 patients had pets at home and got POI, whereas 24 had pets but didn't get POI. Of the 116 patients that didn't have pets, 20 got POI and 96 didn't. We now stratify this original "crude" table into two new tables; one where all the patients have the potential confounder/effect modifier, and one where noone has the potential confounder/effect modifier. Stratified after smoking status:   It is noticed, that in both strata there is a strong connection between exposure (pets) and outcome (POI) since both OR values of 5.00 and 3.77 are significantly above 1 (1 is not included in either of the two 95 % confidence intervals), meaning that for eg. a smoker will have 5.00 times higher odds of getting POI if he/she had pets at home compared with not having had pets at home. First we check whether smoking status could be an effect modifier: This is done by comparing the two OR values from the strata with each other:  The ratio of the two OR values is calculated and is 1.3265. This number is not statistically different from 1 on a 5% significance level, because the p-value is 0.7016, which is far above 0.05. And the number 1 is included in the 95% confidence interval of the odds ratio ratio (ORR). So we can't reject the null hypothesis H0 that claimed that there is no significant difference between the OR values. Therefore smoking status is not an effect modifier for the connection between having pets and getting POI. For if it had been an effect modifier, there would have been significant difference between the OR values of the strata. Note that if smoking status had in fact been an effect modifier, then we would stopped here and proceeded no further (since something cannot be both an effect modfier and a confounder at the same time). But now, knowing that smoking isn't an effect modifier, we can proceed to check if it's a confounder:  The weighted estimate is calculated over the OR values of the two strata. The weighted estimate is WE = 4.2345. This value is then compared with the crude OR value of 7.1111. The crude OR value is the OR value we would have obtained if we hadn't stratified after smoking status into two tables, but kept all data in the original single 2 × 2 table. In this case, there is a clear deviation between the WE and the crude value and therefore smoking status is a confounder for the connection between having pets and getting POI. There is no clear concensus on how much WE and crude have to differ in order to acknowledge the variable stratified after as being a confounder. A rule of thumb is; if the values differ 20% or more then it's a confounder. After having detected the confounder "smoking status" we now know that the the weighted estimate of the two strata, namely 4.2345, is the true effect that the exposure (pets) has on the outcome (POI), after having adjusted for the confounding effect of smoking status. For more infos and formulas about the weighted estimate, please see the page formulas. Note: For something to be a confounder it must fulfill the confounder triangle:  In other words, a variable must fulfill these criteria to be a confounder (C):
 This table can be entered either in Risk & Odds or on this page by entering only into one strata. The OR value obtained from this table is 6.00 (95 % CI [3.19 : 11.29] p-value 0.00). So this OR value is significantly different from 1, therefore there is a connection between C and D and the arrow is established. The arrow E ↔ C can be established by combining the two strata into this one table over E and C: 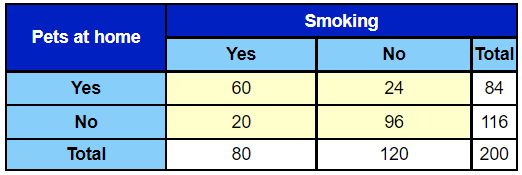 The OR value of this table is 12.00 (95% CI [6.11 : 23.58] p-value 0.00). So the connection between E and C is now also established, since this OR value is significantly different from 1. So there is a strong correlation between smoking and having pets in this fictive, made-up example. The last criteria in the confounder triangle (The potential confounder must not be an effect modfier) was already established earlier by comparing the OR values from the two strata with each other and noticing that they were significantly different. |
|
|
No. of strata:
|
Decimals:
|
|||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||