Regression Analysis
Explanations & examples: If the data in your text file looks like this:
If the data in your text file looks like this: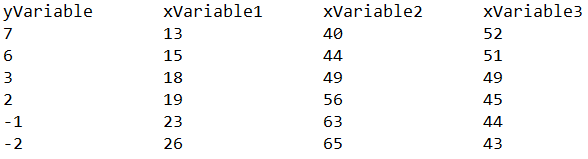 Then you should choose the option "data in file is in columns" to the right when copy/pasting or uploading. If, on the other hand, the data in your text file looks like this: 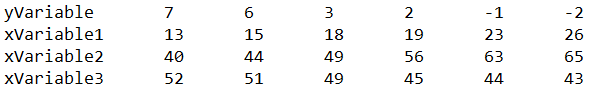 Then you should choose the option "data in file is in rows" to the right when copy/pasting or uploading. Linear Regression:When doing linear regression between one dependent variable Y and one or more independent variables (X1, X2, X3, ... ) we investigate whether there's a linear connection between the X variables and the Y variable. If there is such a connection, a change in the values of the X variables will lead to a change of the Y variable (because Y will then be linearly dependent on the X variables). When performing the linear regression, the beta-values (slopes) of each of the X variables are being calculated. These beta (β) values are the coefficients that are written before the X's in the linear equation of the model. In the case of 3 independent X variables the model will then be: $$ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \epsilon $$ The ε term at the end is an error term (the residual) due to the fact that there may not be a perfect linear connection between the X's and the Y, so that Y isn't perfectly predicted by the X variables but that there's a small distance between the predicted Y value from the expression \( \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 \) and the actual Y-value, namely Y. The distance is ε. If there had been a perfect linear relationship between Y and X, the error would be zero and would be omitted from the model. In this case all the points on the form (x1, x2, x3, ... , y) would lie perfectly on a straight line (evt. in more than 2 dimensions) and all the residuals (distances from the y-values to the straight line) would be exactly 0.The f-test in the linear regression with f-value and p-value is a test to see whether all the involved β values could be equal to zero at the same time. If we cannot reject this null hypothesis (namely if p > 0.05) then the entire model is invalid as a whole (because all the slopes could be zero) and there's no need to proceed any further. A p-value under 0.05 in this test means that at least one β-value is statistically different from 0 on a 5% significance level. After having found the β values for the X-variable with regression, the interpretation of each β value is that this is how much the corresponding X variable contributes to the change in the Y values: If all the other the X variables remain constant, then an increase in the corresponding X variable by 1 will lead to an increase in the Y variable with β (or decrease if β is negative). The intercept or intersection (β0) is the value that Y has according to the model when all the X's are 0. It's the point on the Y-axis where the graph goes through. For each β value the null hypothesis H0 should be tested that β = 0 through a t-test with corresponding p-value. If the p-value is above 5% (p > 0.05) then it cannot be rejected that the β value in question could be equal to 0. A β value of 0 means that the X variable of the β value has no significant effect on the changing Y-values and therefore doesn't contribute significantly to the model. And therefore this X variable should be omitted from the data set and a new linear regression be performed. This procedure should be continued until all the remaining X variables involved have β-values with p-values less than 0.05 (for then it can be rejected that they could be zero). An X-variable can be left out when performing regression by unchecking the checkbox to the left of the headline. It can also be deleted completely by clicking the cross to the right. This procedure eliminating non-significant X-variables from the model is called backwards stepwise regression. The final model involves only X-variables (with their β values) that have a significant effect on the Y variable. Conditions for performing linear regression: There are a couple of conditions on the data involved that have to be fulfilled before performing a linear regression. If one or more of these conditions can't be established, the linear regression shouldn't be carried out. 1. Linear correlation between each single one of the involved X-variable and the Y-variable. 2. The residuals have constant variance (homoscedasticity). 3. The residuals are independent of each other. 4. The residuals are normally distributed. These conditions can be checked in the following way:
 Is there a linear connection between the systolic blood pressure Y and the following 3 X-variables: X1: The age in years x2: Taking a certain type of medicine (in milligrams) X3: The weight in pounds When performing linear regression on the data we get the following output:   As can be seen, the p-value of the β value belonging to X2 (medicine) is above 0.05, therefore this variable doesn't contribute significantly and it can be left out of the model and a new linear regression be performed with the two remaining variables:   This time, all the remaining β values have p-values below 0.05 and are therefore significant. The final equation of the linear model is therefore: $$ Y = 30.9941 + 0.8614 X_1 + 0.3349 X_2 $$ where X1 is the age in years and X2 is the weight in pounds. Logistic Regression:In binary logistic regression, the Y variable can only take two values, nameley 0 and 1. Often, 1 = outcome (disease) and 0 = not outcome (healthy). If there are for eg. 3 X-variables in the model, the logistic model will have the following equation: $$ p(x_1, x_2, x_3) = \frac{1}{1 + \text{e}^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3)}} $$ where p(x1, x2, x3) is the probability that y = 1 given the beta-values and a chosen set of values for X1, X2 and X3. p(x1, x2, x3) can only take values between 0 and 1. Since we're dealing with OR (odds ratios) values in logistic regression, the above equation can also be written in its odds ratio version: $$ Odds = \text{e}^{\beta_0} \times \text{e}^{\beta_1 x_1} \times \text{e}^{\beta_2 x_2} \times \text{e}^{\beta_3 x_3} = OR_0 \times OR_1^{x_1} \times OR_2^{x_2} \times OR_3^{x_3} $$ The task is to find the specific values of β0,β1,β2 and β3 that will maximize the probability of getting the current observed values of Y given the values of the X-variables in the data set. This is not as straightforward as with linear regression since there is no formula for finding the beta-values. Instead a method is used called maximizing the log-likelihood where the most optimal values for the betas is found satisfying a desired level of precision. By taking the logarithm on both side in the above equation we get $$ \ln(odds) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 , $$ thus, the interpretation of each β-value in front of the corresponding X-variables, for eg. β1, is that the logarithm of the odds will increase by this much when the value of X1 increases by 1 (all the other X remaining the same). In the odds ratio version of the equation mentioned earlier, the interpretation of the OR values corresponding to each X-variable is that every time the value of x increases by 1 (the value of all other X-variables remaining the same), the outcome odds will get OR times higher than before. If all the x's in the equation have the value 0, we get that: $$ Odds = OR_0 \times OR_1^{0} \times OR_2^{0} \times OR_3^{0} = OR_0 \times 1 \times 1 \times 1 = OR_0 $$ Therefore, the value of OR0 can be interpreted as a "baseline" or "reference", namely as the odds that you would have of getting the outcome, if you have the value 0 in all of the involved risk factors (the X-variables). A different baseline can be chosen, however, where the values of each of the x are not zero, for eg. x1 = 17, x2 = 3.5, x3 = 50 etc. And the values of OR0 will then be changed accordingly. Also in logistic regression each β-value can be tested with a t-test to see if it could be equal to zero. If this is the case (p > 0.05) then the X-variable in question should be deleted from the model. When performing logistic regression on a data set all the involved X-variables should be normally distributed and independent of each other (when one X-variable has a certain value, this info may not influence the values of the other X-variables). The chi-squared-test in logistic regression (the "overall model fit") is a test to see if all the beta-values could be equal to zero at the same time. If so (when p > 0.05) the whole model is invalid and should be discarded. A p-value under 0.05 in this test means that at least one β-value is statistically different from 0. Example: In the following data set, the outcome (Y) is either 1 = getting the disease or 0 = not getting the disease.  There are two explanatory X-variables, X1 = receiving a certain medication (1 yes, 0 no) and X2 = the person's age in years. It will be investigated whether the X-variables have a significant effect on the odds of getting the disease:   The current model according to the output would then be: $$ Odds = \text{e}^{-6.3635} \times \text{e}^{-1.0241 x_1} \times \text{e}^{0.1190 x_2} = 0.0017 \times 0.3591^{x_1} \times 1.1264^{x_2} $$ Note, however, that the p-value of the beta-value β1 has a p-value of 0.3818, which is more than 0.05. Therefore the variable medication does not contribute significantly to the model (has no significant effect on the odds of getting the disease). Therefore this this variable should be left out of the model:   Now the remaining variable (Age) has a beta-value with a p-value below 0.05 and is therefore significant. The final model will then be: $$ Odds = \text{e}^{-7.0925} \times \text{e}^{0.1246 x_1} = 0.0008 \times 1.1327^{x_1} $$ So, in the final model of this example the odds of getting the disease is determined by the patients age alone. The odds of a 45-year-old of getting the disease would then be; $$ Odds = 0.0008 \times 1.1327^{45} = 0.2179 $$ Converted into risk this will be \( risk = \frac{odds}{1 + odds} = \frac{0.2179}{1.2179} = 0.1789 = 17.89 % \) risk of getting the disease. The odds ratio (OR) of a 50-year-old relative to a 45-year-old: $$ OR = \frac{odds_{50}}{odds_{45}} = \frac{0.0008 \times 1.1327^{50}}{0.0008 \times 1.1327^{45}} = \frac{0.4063}{0.2179} = 1.8646 $$ A 50-year-old has a 1.8646 times higher odds of getting the disease compared with a 45-year-old. To see the formulas used in the calculations please see the page formulas. |
Regression Type: Linear Regression Logistic Regression |
No. of X-variables: |
No. of rows: |
Decimals:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



